From http://fivethirtyeight.com/features/the-puzzle-of-the-lonesome-king/.

A coronation probability puzzle from Charles Steinhardt:

The childless King of Solitaria lives alone in his castle. Overly lonely, the king one day offers one lucky subject the chance to be prince or princess for a day. The loyal subjects leap at the opportunity, having heard tales of the opulent castle and decadent meals that will be lavished upon them. The subjects assemble on the village green, hoping to be chosen.

The winner is chosen through the following game. In the first round, every subject simultaneously chooses a random other subject on the green. (It’s possible, of course, that some subjects will be chosen by more than one other subject.) Everybody chosen is eliminated. (Not killed or anything, just sent back to their hovels.) In each successive round, the subjects who are still in contention simultaneously choose a random remaining subject, and again everybody chosen is eliminated. If there is eventually exactly one subject remaining at the end of a round, he or she wins and heads straight to the castle for f?ting. However, it’s also possible that everybody could be eliminated in the last round, in which case nobody wins and the king remains alone. If the kingdom has a population of 56,000 (not including the king), is it more likely that a prince or princess will be crowned or that nobody will win?

Extra credit: How does the answer change for a kingdom of arbitrary size?

##My Answer##

This is a problem easily solved by simulation.

We’ll start by setting up a few variables:

n_subjects <- subjects_remaining <- 56000
subjects_in_competition <- c(1:n_subjects)

Now, we’ll run a loop removing all those chosen by a random number initiator.

while (subjects_remaining > 1){
    chosen_subjects <- sample(1:subjects_remaining, replace=TRUE)
    subjects_in_competition<-subjects_in_competition[-chosen_subjects]
    subjects_remaining<-length(subjects_in_competition)
}

The first time we run this, we get: subjects_remaining = 1.

To get a proportion of times that a subject is crowned vs. the king remains lonely, we’ll repeat this often, using the above loop as a function.

subjects_in_competition <- c(1:n_subjects)
nreps<-1000
cl <- makeCluster(detectCores() - 1)
registerDoParallel(cl)
 
subs_crowned<-foreach(1:nreps, .combine = sum) %dopar% removerLoop(subjects_in_competition)

stopCluster(cl)
prop_crowned<-subs_crowned/nreps

This gives us a winning subject proportion of 0.675.

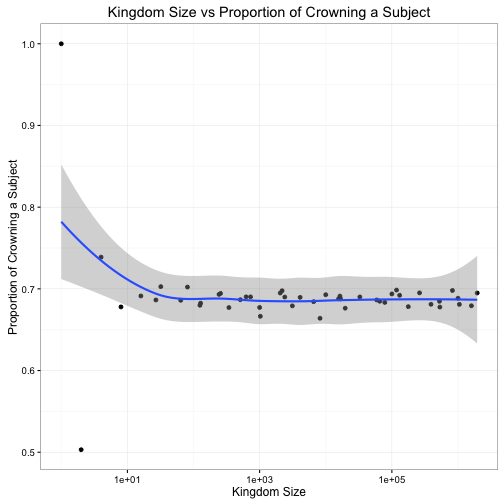
For an arbitrary kingdom size, we can repeat this. We could repeat the above task for every kingdom size from one to one million, and plot the proportions to try understand the trend. I’m using a series of exponential values to get a pseudo-random selection of kingdom sizes, hopefully this isn’t picking up any artificially present corellations.

par_simulate<-function(n_subjects, nreps=10000){
    subjects_in_competition <- c(1:n_subjects)
    cl <- makeCluster(detectCores() - 1)
    registerDoParallel(cl)
    subs_crowned<-foreach(1:nreps, .combine = sum, .export=c("removerLoop")) %dopar% removerLoop(subjects_in_competition)
    
    stopCluster(cl)
    return(subs_crowned/nreps)
}
 
sub_size<-unique(c(2^(0:20), 3^(3:13), 5^(3:9), 7^(3:7), 10^(3:6)))
propcrowned<-numeric()
for(i in sub_size){
    propcrowned<-c(propcrowned,par_simulate(i, 10000))
}

## Warning: closing unused connection 5 (<-localhost:11243)

## Warning: closing unused connection 4 (<-localhost:11243)

## Warning: closing unused connection 3 (<-localhost:11243)

prop_size<-data.frame('Subjects'=sub_size, 'Proportion'=propcrowned)

This likely takes a while.

But, we can now plot our results:

ggplot(prop_size, aes(x=Subjects, y=Proportion)) +
    geom_point() +
    geom_smooth() +
    scale_x_log10() +
    theme_bw() +
    ggtitle("Kingdom Size vs Proportion of Crowning a Subject") +
    xlab("Kingdom Size") +
    ylab("Proportion of Crowning a Subject") +
    scale_colour_brewer(palette = "Dark2")